地震と活断層（16）：摩擦の追憶

update 2004.5/16

どう摩擦係数ってどうよ？

　静止摩擦に、、、

動摩擦ってやつですね。習ったなあ。

　あーそういえば習いましたね。高校の時に。摩擦係数には２つあって、止まっている時の摩擦係数は動いている時の摩擦係数より大きいって、あれでしょ。とっくに知ってますよ～と思ったことでしょう。でも実際にはそんなに単純じゃないのです。摩擦係数は速度によって大きく変化するのです。早ければ早いほど小さくなるし、遅ければ遅いほど大きくなるのです。つまりたった２つ（動摩擦係数と静止摩擦係数）じゃないってことです。っていうか摩擦係数は速度によってダイナミックにどんどん変化するので、動摩擦係数も静止摩擦係数といった決まったものは存在しないのです（注：過言です）

ちょ、ちょっと待って下さい。動いている方はどんどん高速になるほど摩擦係数が小さくなるとして、動摩擦係数がイロイロというのは良しとしましょう。でも、止まっているのは、速度ゼロは１つしかないので、静止摩擦係数はやっぱ１つなんじゃないでしょうか？　いいえ違います。

遅さの概念

このテの話で大事なのは、「遅さ」の概念です。「速さ」は良く知ってますね。時速２ｋｍとか３００ｋｍといったやつですね。なじみ深いのはｋｍ／時ですね。距離／時間。ある時間内にどれだけの距離移動できるか？って奴です。速度です。で、これに対して「遅さ」は時間／距離で表します。いわば遅度でしょう。そんなのただの速度の逆数じゃん。意味なーし。と、思ったことでしょう。でも、そこが違うのです。全く違うのです。この遅度は、果てしなく遅い速さを扱える画期的な概念なのです。

　遅さっていう速度は、停止している物の速度も表現できるのです。これがポイントだねえ。

　速度だったら、止まっている物の速度はゼロ。０ｋｍ／時ですね。たった今、停止した車も、昨日から駐車してある車も、１０年前から放置してある車も同じ速度ですね。でも遅度なら停止してからの時間。放置時間を表現できます。信号で一旦停止してから１ｋｍ動いた車は、１分／ｋｍでしょう。昨日から駐車してある車が１ｋｍ走ったら、２４時間／ｋｍ。１０年放置されていた車が急に走れば１０年／ｋｍですね。これが速さならどれもゼロになってしまうところです。でも遅度なら一緒じゃない。

前回の地震から１００年経った断層と地震直後の断層の摩擦係数を比較する上で重要なのは、こっち。遅さですね。

摩擦の追憶：メモリー効果

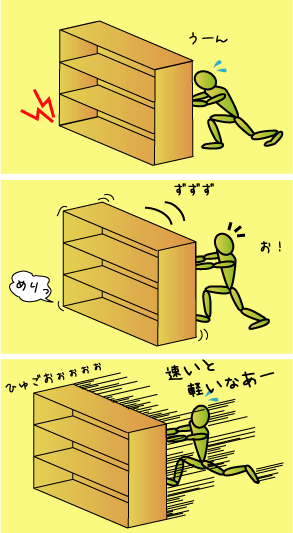　永年置きっぱなしのタンスを動かします。ぐぐぐっ、、メリッ。これが臨界すべりって奴ですね。

　断層を考える上で重要な摩擦現象のひとつにメモリー効果があります。メモリー効果といえば、ケータイやノートパソコンのバッテリーのメモリー効果がありますが、全く関係ありません。早く燃料電池が実用化されて欲しいですね（←本題と関係ない）。

　さて、止まっている物体を急に動かそうとすると、ちょこっとすべってから急激に加速します。このちょこっとの距離を臨界すべり距離と言います。これはラビノヴィッツというおっさんが、斜面に物体を置いて、それにボールをぶつけて急激に加速させる実験で観察されたことです。身近な例で示しますと、何年も置いてあるタンスを動かそうとすると、やたら重いのです。で、満身の力を込めると「メリッ」といって剥がれます。そしたらつ、つ、つと動き始めます。もし部屋が体育館のように広ければ、どんどん押すことができます。加速すればするほどタンスはする、する、する、と動くことでしょう。でもあなたが普段の暴飲暴食と寝不足のせいで息切れすると、急激にタンスは重くなり、停止してしまうことでしょう。で、何の話かと言うと、最初の「ばり」が臨界すべり距離をすべっているところなんですね。そんで加速につれて摩擦が小さくなってするするすべったり、息切れして減速とともに摩擦が大きくなるのが、摩擦の速度依存性ですね。で、動き始めの「バリッ」の摩擦力がタンスの放置時間によるってわけです。つまりさっきの遅度の話ですね。昨日置いたタンスと１０年も放置してあったタンスとでは、１０年もののタンスの方が圧倒的に遅いので、摩擦力が強いってことです。つまり摩擦表面がそれまでの放置時間を記憶していて、臨界すべり距離をすべる間は、それまでの放置時間に依存する摩擦力を持つのです。そして臨界すべり距離を超えると初めて加速し始めて、新しい表面の状態に進化し、摩擦係数は減少していきます。しかも最初の「バリッ」に必要な摩擦力というのは、例えば臨界すべり距離を２ｍｍとしたら、１００年放置してから２ｍｍ進むのと、１００年かけてじわーっっっと２ｍｍ進むのと同じ大きさの力がいるのです。１００年たって動くものも、１００年かけて動くのも同じ。つまり止まっている物も、限りなく遅く動いている物も、等価である（臨界すべり距離内の摩擦力に関して）ということです。

これがメモリー効果です。ついさっき設置したタンスも１億年前から設置してあるタンスも、大きさや重さが一緒なら、動かす分には一見同じかと思いきや、床との接触表面が、これまでのいきさつをしっかりと覚えているんですね。

またもアスペリティ

さて、なぜそんなことが起きるのでしょうか？　まず、この手の話のトリックは擬人化にあるのです。物体には意志なぞないのに、何かを考えて振る舞っているかのように例えるから、不思議な気がするのです。断層も台風もただの自働機械であり、メカニズムとコンディションに従って、単に作動しているにすぎないのです。

では、摩擦の速度依存性やメモリー効果はどうやって起きるのでしょうか？　ディートリッヒというおっさんの考えによれば、次のようになります。もともとこの手の摩擦実験は金属同士を接触させて行われていたので、とりあえず金属を念頭にして考えましょう（岩石だとやや複雑になるので）。

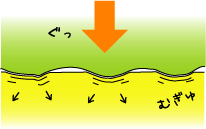　ゆっくりすべる（または止まってる）とアスペリティがじわーって変形して、接触面積が増えます。

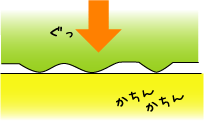　逆に速く動いていると、食い込むヒマがないので接触面積が小さくなります。ってことは摩擦が小さいってことですね。

まず、やっぱアスペリティを前提とします（第１４回を思い出そう）。どんな表面も完璧な平面ではなく、ちょっとした凸同士が接触して全体を支えています。第１３回の時の摩擦の垂直応力依存性は、重さによってアスペリティが増加するって説明だったけど、今回の場合は重さは変わりません。でも、時間が経つにつれて徐々にアスペリティが増えるのです。どーやって増えるかといえば、この実験の場合、金属板なので接触している凸がグニャリと塑性変形するのです。

塑性変形ってのは、短期間にグッと力を入れても弾性的（第５回、第６回参照）にしか曲がらない金属棒も、少しの力でも長ーい時間かけ続けていると、ついにはゆっくりと曲がって奴です。この手の性質はアメやチョコの方が顕著ですね。ゆっくり曲げたらグニャリと曲がるのに、さっと曲げると強く反発して、ついには折れてしまう、だけど小さな差応力であっても長ーい時間かけるとゆっくりと曲がる、、、ね。

　つまりアスペリティも時間とともにゆっくりと変形して、より広いエリアがくっついていく。つまりアスペリティの増加であり、摩擦の増加なわけです。また逆に、接触時間が短ければ凸はあまり食い込めないので、摩擦は小さいでしょう。これを前回の摩擦係数μで言えば、貫入硬さに時間依存性があり、長期的には貫入硬さは小さくなる。ってなわけです。

追憶もアスペリティで

　これが止まっていた時のアスペリティとしましょう。がっちり食い込んでます。

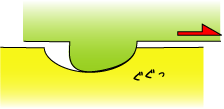　で、臨界すべりってのは、こいつを乗り越えてる最中の摩擦です。この時の摩擦はそれまでどれだけ食い込んでいたかによって強くなります。これまでのいきさつがメモリー効果ってわけですね。

　くどいよーだけど、一応メモリー効果や遅さと停止しているものとの等価関係の話もアスペリティを使って説明しておきましょう。長い間接していると徐々にアスペリティは食い込んでいって、強い摩擦力を持つようになります（右図上）。タンスで言えば、長いこと放置してあったタンスを急に動かす時の臨界すべりの摩擦力は放置時間によって変わるでしょう。１０ヶ月よりも１００年放置されたタンスの方がアスペリティは大きく成長するでしょうから。加速してしまえば、一緒なんですがね。でも、立ち上がりにかかる力が違うんですよ。だから摩擦力は時間と共変化するので、まるで過去を覚えているかのような気がするのです（もちろん物の表面は物思いにふけりません。ただ状態が変わったにすぎないのです）。

そして１００年放置していたタンスを動かす時の摩擦力は（つまり臨界すべりの間の摩擦力）は、１００年かけて同じ距離をゆっっっくりすべるのと同じくらい強い力なのです。これがゆっくりも停止も等価って意味です。

それはまるで、夏休み明けの仕事はダルイですが、休みを取らずに同じ期間に少しの仕事をゆーっっくりやっても、やっぱり同じくらいダルイみたいなもんですね（よけーわからん）。

今回は下記の教科書を参考にさせていただきました。
ショルツ　著／柳谷俊　訳　　「地震と断層の力学」