地震と活断層（９）：モール円の美

update 2002.8/16

　モールの応力円とは何か？

物体内部にはいろんな向きのグリフィスクラックが無数に存在していて、そのぜーんぶの応力状態をシンプルに表現できるもの。それがモールの応力円なのです。

　　さて今日はモールの応力円ですが、私は自分が２回生の授業で初めて習った時にはさっぱりわからんかったなああ。特にでも、これはとても便利で優れ物なのです。そこで数式は使わずにコンセプトの理解を中心に話を進めたいと思います。

モールの応力円というのは、モールというおっさんが思いついためちゃ便利なもので、物体中の全ての角度の全てのグリフィスクラックの応力状態が表現できるっつー代物なのです。しかもこいつはどんな深度の断層でも対応できる優れもので、ぜひ自由自在に使えるようになってください。で、このモールの応力円（単にモール円とも言う）は横軸を垂直応力、縦軸を剪断応力で表します。ん？どっかで見たグラフですね。はい。クーロンの破壊基準と同じグラフです。そんでまた右図のようにまた封圧がかかっている岩石に差応力をかけていきます（地下深部の岩石にテクトニックな力をかけたようなもんです）。そして岩石中にはあらゆる方向にグリフィスクラックが入っています。で、このいろんな角度に入っているクラックにどんだけ剪断応力がかかるのか、つまりどれがすべり易くて、破壊のきっかけになるのかを考えよーってわけです。で、答えから言いますと、このグラフに円として表現できます。あらゆるグリフィスクラックの面上の応力状態は、この円周上にプロットされるのです。決して円の内側や外側にはありません。

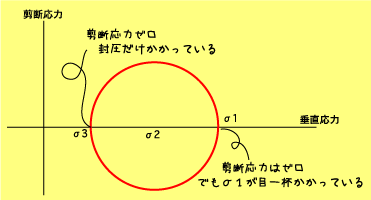物体内部のすべてのグリフィスクラックの面にかかる応力は（垂直応力と剪断応力の両方が！）全てがモール円の円周上にプロットされます。

　では、なぜ円になるのでしょうか？　数式的な証明はいろんな教科書に載っているので、そっちを見てください。それを見ながら式を展開していくとわかりますが、途中から明らかに円の方程式を目指して進んでいきます。つまりモールのおっさんには最初から円だとわかっていたんですね。ちょうどセンター試験の数学でも数式を解く前に選択肢を見ただけで答えがわかる人がいるのと同じです（私は決してできないが）。
「これは、、、、４だな」
「ほら！」
みたいな。きっとモールという人もそんな感じだったんじゃないでしょうか。と、いうわけでまず直感で、なぜ円になるのかを理解しましょう。

　　物体の中には、いろんな角度のクラックがあるんだけど、もっっっとも剪断応力が大きいのはどれでしょう？はい。σ１に対して斜めのクラックです。これは簡単ですね。ではσ１（第６回目参照）に対して垂直な面では？もしくは平行な面では？応力というのは面に対する力ですから（第５回参照）ちょうど風に対するヨットの帆のようなもんです。そこで下図のように考えます。岸壁に留まっているヨットに風が吹き付けるのですが、帆に対して平行な風だと帆に風が当たりませんのでヨットをずり動かせる力、つまり剪断応力はゼロです。でも、大気圧だけはかかっているので、σ３はゼロではない。次に帆に垂直な方向から風が当たっていたらどうでしょう？　帆は目一杯風を受けていますが、ヨットは岸壁に押し付けられるのみで、やっぱりずり動きません。剪断応力はゼロです。でも帆は大気圧＋風圧（封圧＋風圧：読者を混乱させるダジャレ）を受けていますので、垂直応力は最大になります。で、本命の斜めからの風ですと、はじめてヨットは垂直応力と剪断応力を受けて動くのです。こん時の垂直応力はさっきの平行な風と垂直な風との中間だし、剪断応力は４５°の時に最大で、０および９０°の時にゼロとなるってわけです。だからその前の図のように、あらゆる向きの時の応力状態（垂直応力と剪断応力）は円周上にプロットされるのです。

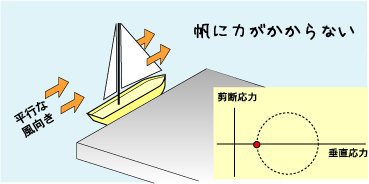
え、なんで着岸しているヨットを例えに使うのかって？　着岸してたら動くはずないんだけど、断層は２つの面の剪断作用だし、面にかかる力（応力）は帆を例えにするとわかり易いからです。 　で、この図のように平行な風だと帆に力がかかりません。風を受ける面積がゼロだからですね。まあ、あえて言えば帆にかかっている力は大気圧だけですね。

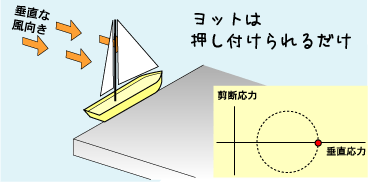帆に垂直な風だと　大気圧＋風の力　ですね。垂直応力は最大！ですが剪断応力はゼロ。

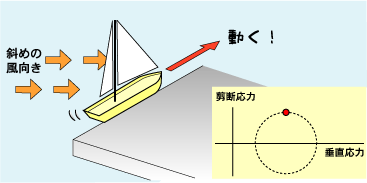斜めの風で初めて剪断応力が発生します。平行な風から少しずつ斜めの風になると、徐々に剪断応力が増して、垂直に近付いていくと徐々に減っていきます。

　美への仕掛け　

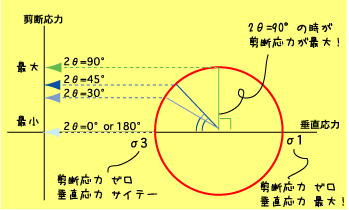σ１からの角度θを２倍にして表現します。そーするとθ＝４５°（ってことは２θ＝９０°）はモール円の頂上なので、剪断応力が最大に！　そんでそれよりも傾斜が緩くても、きつくても剪断応力は減少して、θ＝０°もθ＝９０°も剪断応力はちゃーんとゼロになります。

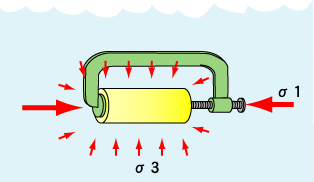クランプで岩石試料を挟んで、ギリギリと締め上げて、ついにはバキッって壊れるんですな。この時、クランプの軸の方向がσ１で、そこから45°の方向のグリフィスクラックの剪断応力が最大になるってわけです（でも、実際には45°じゃなくて30°くらいの方向で割れるんですな。理由？それは最後に）。

　で、モール円にはもう１点うまい仕掛けがしてあります。円の中心からの角度がσ１からの角度の２倍に相当するのです。なぜ２倍になるのかって？　そりゃ愚問というものです。なにせ、そうなるように仕向けられているんですから。物体中のある面のσ１に対する角度をθ（シータ）とすると、円の中心からの角度を２θとしてあります。するとどんな良いことがあるのか！　それは任意の角度の面の応力状態がちゃーんと表現されるのです。簡単に言えばθ＝４５°の時に剪断応力は最大になるんですが、モール円上では、２θ＝９０°なので、右図のモール円の一番上にプロットされます。ほら、剪断応力最大でしょ。そしてθ＝０°（σ１に平行）な時は、２θ＝０どなので、面には垂直応力として封圧はかかる剪断応力はゼロ。そんでθ＝９０°（σ１に直交）な時は、２θ＝１８０°になって、こいつも剪断応力はゼロ。でも垂直応力は最大になるわけですね。ね、ほらうまくできているでしょ。

　ところで、クランプによる破壊や、ヨットをずり動かす力や、断層運動を考える時には右図のような状況が大事でした（覚えてる？）。周囲から均等にかかる封圧と、それに加算される力。ヨットで言えば　大気圧＋風圧　ですね。この「差」を差応力といいます。この差が大きいほど、破壊つまり剪断応力が大きくなるのです。たとえσ１が１００ＭＰａだろうと１ＧＰａだろうと、封圧も同じだけあれば破壊は生じないのです。ある小石が室内でクランプで５ＭＰａかけたら壊れるとして、こいつを海底に放り込んだとしましょう。室内で差応力５ＭＰａくらいで壊れる小石であっても、周囲から均等に水圧がかかるのであれば、それが２０ＭＰａでも１００ＭＰａでも壊れないです。深海底に小石が落ちていても、バキッって壊れないのです。いやあ、差応力って偉いなあ。

で、この差応力というのはσ１とσ３との「差」なので、モール円で言えば円の直径なのです。さっきの小石の話をモール円で表現するとこうなります。室内の封圧は、大気圧なので、ほとんどゼロとしましょう。クランプでつぶす前は差応力はゼロなので、円の直径もゼロ。クランプに力をかけると円の直径は大きくなります。でも、σ３つまり大気圧は一定なので、σ３の位置はかわらずに、σ１が左に移動して円の直径が大きくなるのです。

　だからこれを海底に沈めたら水圧、つまり封圧が増えるのでσ３が右へと移動します。この時点でクランプのネジを締め付けてなければモール円の直径はゼロ。で、ギリギリと締め付けると、σ１がもっと右に移動し始めてモール円の直径が大きくなるってわけですね。そんで差応力が大きくなっていって最後には破壊に至るって訳です。物体内部の応力状況がこのモール円だと実にうまく表現できるでしょ？　

クーロンとの出会い

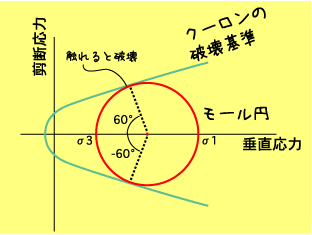クーロンと組み合わせるとこーなります。破壊基準以下の応力状態なら決して壊れません。でもちょっとでも触れると壊れます。封圧、差応力、剪断強度、剪断面の角度などがいっぺんに表現されてます。

　次はいよいよ差応力が大きくなって（＝モール円が大きくなって）破壊に至る話と、モール円はなんて便利なんだという話です。さてモール円は、縦軸を剪断応力、横軸を垂直応力で表現しました。っていうことは第８回のクーロンの破壊基準で出てきたグラフと一緒なわけです。つまり双方は同じグラフ上にプロットする事ができるってわけです。クーロンの破壊基準を思い出してください。あの粘土の剪断実験を。破壊基準に達しない応力状態（クーロンの線の下側）では、どんな応力状態であっても、グラフのどこにプロットされても断固破壊しないのです。つまりモール円がクーロンの破壊基準線の下側にある場合は破壊しないってことです。右図のように。このままではこのまんまです。何億年たっても破壊しないのですが、差応力を掛けていきますと（いつもの水中クランプモデルだとネジをしめるってこと）、モール円が徐々に大きくなっていってついにクーロンの破壊基準に触れてしまいます。そーするとついに破壊！してしまうのです。

この時重要なことはモール円は２θ＝６０°くらいの場所でクーロンの破壊基準に触れるってことです。つまりθ＝３０°ってことです。つまり右図のような状態で岩石を破壊するとσ１に対して３０°くらいの角度で割れるのはこうしたわけなんですね。剪断応力が最大になるのは４５°なのに実際には３０°くらいで割れるのはクーロンの破壊基準が斜めのためなんですね（垂直加重に比例して剪断強度が増すというのは摩擦と同じ特徴ですが、それはまた後日）。また例えばプレート沈み込み帯の付加体の先端にも非常に低角のスラストが発達しているんですがこれも、海洋プレートが横からぐいぐい押してきてσ１が水平にあるから、断層も水平から３０°以内という低角な連中ばかりなんですなあ。

では、次回はこのモール円をいよいよ断層に応用してみましょう。

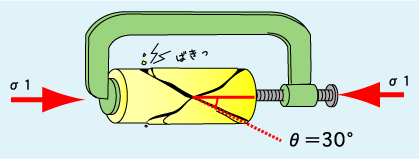さっきの答えです。σ1に対してなぜ約30°で割れるのか？　なぜ45°じゃないのか？　ですが、それはクーロンの破壊基準が斜めだから。難しく言えば垂直応力に応じて剪断強度が増すからですね。もし垂直応力に関係なく剪断応力が一定だったら45°で割れるでしょう（ただし、それって摩擦の法則に従わないってことですがね）。

今回は下記の教科書を参考にさせていただきました。
Ｊ．Ｅ．ゴードン著　土井恒成　訳　「強さの秘密」
粟津清蔵　監修　「絵とき土質力学」
狩野謙一、村田明広　著　「構造地質学」