地震と活断層（10）：スリッププレディクタブルモデルはありえない

update 2003.9/7

タイムプレディクタブルモデルが力学的に妥当だ

　　さて、長いことかかって破壊力学の基礎を学んできましたが、よーやく当初の目的であった、断層の活動について考えてみましょう。で、ちょっと思い出してみましょう。断層はまちまちの時期にバラバラの規模の地震を引き起こすようにも思えるけど、よーく調べてみると規模と周期との間には一定のルールがあって

「前回の地震の規模によって、次の地震の時期が規制されるタイプ：
タイムプレディクタブルモデル」
と
「前回の地震からの経過時間によって、次の地震の規模が規制される：
スリッププレディクタブルモデル」

があるっってことを話しました（第４回参照）。このような活動パターンは、地下深部の断層面上のどんな原因によって引き起こされているのでしょうか？？　具体的には、震源物質の力学的・化学的振る舞いによって説明されるべきなんだけど、それは未だ不明のままなので、まずは力学的なフレームワークで考えてみましょう。

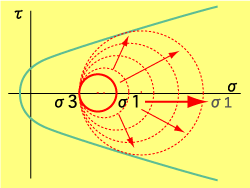σ３は震源断層の深さ分の封圧なので、こいつは地震サイクル中には変わりません。σ１はテクトニックな歪み分なので、刻一刻と増加します。

　　地下数ｋｍ〜数１０ｋｍの深さに地震を起こす断層面があってこれが繰り返し地震を起こすわけです。そこではどんな応力が働いてるかと言えば、まずは封圧ですね。周囲が岩石ですから岩圧と読んでもいいけど、まあ震源を５〜２０ｋｍくらいと仮定したら、だいたい１２０〜５００ＭＰａくらいかかっているとしましょう（σ３ですね）。そんでこれにテクトニックな応力が加わっています（σ１ですね）。沈み込み帯なら水平な圧縮力ですね。海洋プレートが毎年こんこんと沈み込んで、我らの地殻を刻一刻と歪ませています。ですから、この歪みがたまるペースはだいたい一定だと考えましょう。地殻は弾性歪みをこんこんとためつづけます。そーすると弾性歪みの量と差応力とは比例しますので（第６回参照）。モール円で言えば、σ３は変わらずに（深度は変わってませんからね）σ１がせっせと大きくなるのです。するってーと要はモール円がどんどん大きくなるってことですね。そしてついにはクーロンの破壊基準線に接して破壊に至る、地震が起きるってえわけです。

　ここで問題になるのは、
　差応力ゼロ　→　モール円の成長　→　破壊　→　環の最初戻る　

のであれば地震の発生間隔とマグニチュードは一定になるはずです（レギュラースリップモデル）。でも実際の地震は周期はまちまちで、タイムプレディクタブルモデルに従うとすれば、どうなるかっていうと、モール円の成長レートは一定なんですから（こんこんと沈み込むプレートの移動速度に依存するから）、スタート地点が違うってことですね。クーロンの破壊基準に触れて地震が起きて、弾性エネルギーが破壊に消費されるんだけど（第５回参照。表面エネルギーに変換されるんでしたね）、弾性エネルギーは完全には消費されないで破壊が停止する。ここがポイントです。つまり地震の後にモール円の直径がゼロにならないってわけです。消費がちょこっと、つまり小地震だったらモール円はかなり大きいままですから、成長を再開したらすぐに限界になって次の地震が来ます。でも巨大地震が来たら、エネルギーが多量に消費されて、モール円は小さくなって、限界まで成長するのに長ーい時間がかなるってわけです。ほら、タイムプレディクタブルモデルがうまく説明できるでしょ。

あの階段状のグラフの下の線、なぜあの傾きは何なのか不思議でしたが、こーして考えてみると、下線の傾きはモール円の成長速度なんですね。つまりプレートの沈み込み速度によるものだったのですね。プレートの沈み込みによる歪みの蓄積ペースが早ければ、、下線の傾きは大きくなる。すなわちモール円の成長速度が早くなって次の地震がすぐに来るってわけです。

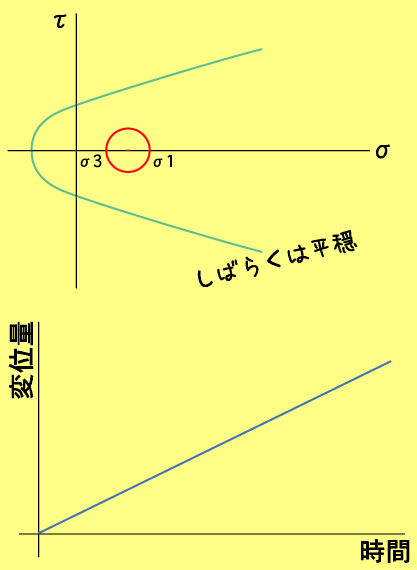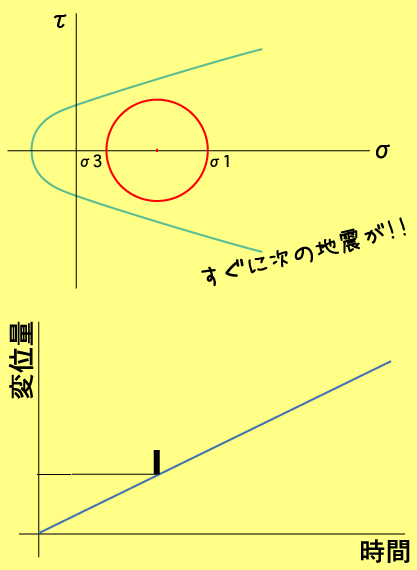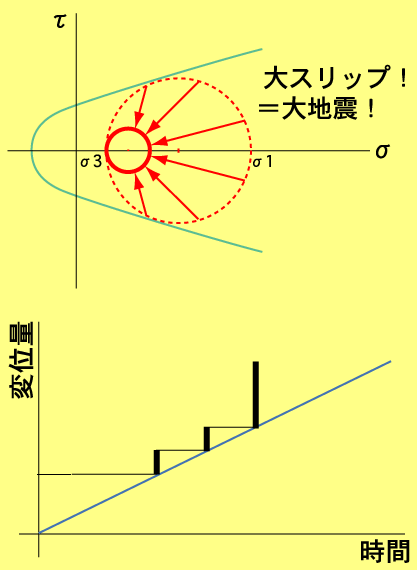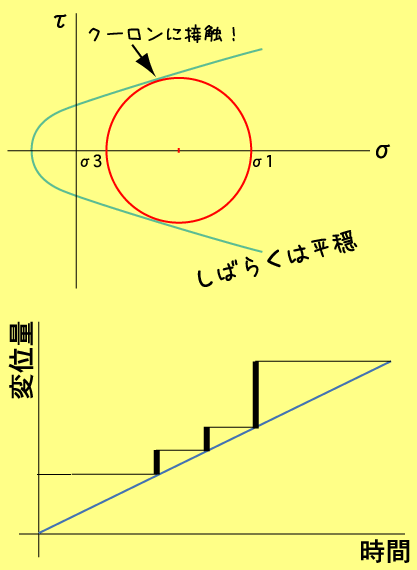
地震のサイクルとその応力状態のアニメです。両者の関係を繰り返し見てみましょう。破壊がどれだけ進行するか、っていうか「どこで止まるか」がキーポイントだってことがわかるでしょ？！

　スリッププレディクタブルはアンエイブル（英語ダジャレ）

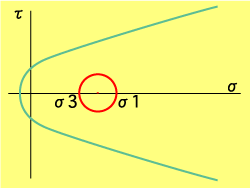いつ破壊するかわからないが、今破壊したら、、ってことは、どんな応力状態でも破壊するって言ってるに等しいわけですよ。上図の応力状態でも破壊するでしょうか。どうも前提から話が噛み合いませんな。

　さてもう一方のスリッププレディクタブルモデルはどーなるのか考えてみましょう。こいつは前回の地震からの経過時間によって、今起きるならこの位の規模の地震が起きるっていうふうに変位量がわかるってわけですね。さっきのタイムプレディクタブルモデルと共通するのは、時間とともに歪みを蓄積するっていう点です。時間とともにモール円が着々と大きくなるという点ですね。そしていつ地震が起きるかはわからないが、起きたならば階段状のグラフの上線に接するまでの大きさの地震が起きるっていうか断層がすべるんですね。つまりこいつの特徴は、

１、常に地震が起きる可能性がある。
２、断層のすべり（もしくは解消するエネルギー）量は毎回の地震で一定である。つまり階段状のグラフの上の線のレベルまですべる（解消する）ってわけです。

ここが重要なポイントです。常にいつでも地震が起こるということはあり得ないということです。スリッププレディクタブルモデルはモール円がクーロンの破壊基準線に接していないにも関わらず破壊するということを仮定している、ということなのです。いつ地震が起こるかわからない（今すぐかも）ということはモール円の直径がたとえゼロでも破壊するかも、、と言っているに等しいのです。だからスリッププレディクタブルモデルは力学的にはあり得ない、と言えるのです。

不可能と言われると覆したくなる

　では、本当にあり得ないのかと言えば、やっぱり普通ならあり得ません。ただし２つだけ可能にする方法あります。モール円の直径を急激に大きくすることはできませんが（プレートの移動速度は瞬間的に加速しないですから）、１つはクーロンの破壊基準を下げること。もう一つは、モール円を直径はそのままでも左に動かすことです。具体的な方法はまたいずれにしましょう。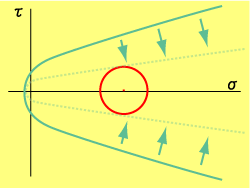

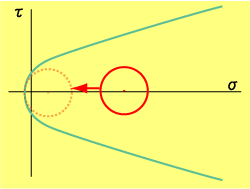とにかくモール円が急に大きくなれないのなら、クーロンの破壊基準を下げるか、モール円の直径はそのままで左に動かす。そうすればモール円とクーロンの基準は接して、無事に（？）破壊することができます。

今回の内容は本サイトオリジナルですので、
より詳細な参考書はありません。