地震と活断層（15）：摩擦ってなによ

update 2004.4/20

それってコーコーで習いました

　　（Ｆ：引きずるのに必要な力　μ：摩擦係数　ｎ：垂直応力）である。

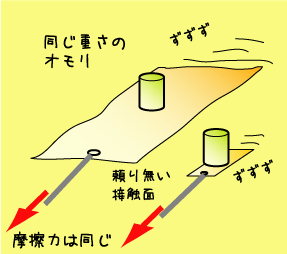　摩擦力が面積にカンケーなし！なんて、信じらんなーい。と、思ったことでしょう。でも、こんな絵を描いてみたら「やっぱそうかも、、」という気がしてきますねえ。

というわけで、前回説明しましたように、摩擦力学に話題を移しましょう。

で、まず摩擦の法則です。高校物理では

摩擦は面積に関係なく、垂直応力に比例する。
摩擦係数には動摩擦係数と静止摩擦係数の２つがある。

そんで、摩擦係数は摩擦面の状態に依存する。

と、習います。でも、これって不思議じゃありませんでした？　まず、（１）の面積に依存しないって点ですが、広ーい面積の板と小ーさな面積の板とで、板の上に乗っているオモリの重さが同じなら、引きずるのに必要な力は同じだっていうんですよ。私はかなり納得いかなかったんですが、右図のようにペラペラの紙の上にオモリを載せたものなら、広い紙のソリも小さな紙のソリも引きずるのに必要な力は同じかもしれません。まあ、ありかなって思えなくもないですね。なるほど本当かもしれません。

　で、次に（２）の２つの摩擦係数ですが、たしかに止まっていたものを加速させるのと、動いている物をさらに加速させるのとでは、必要な力がぜんぜん違います。動いている物の方を加速させる方が断然ラクです。でも、本当はこれだけでは正しくありません。次回述べますが、摩擦係数はあらゆる速さと遅さで変化します（つまりたった２つじゃないってこと）。

アスペリティっていうんだ？　素敵な名前だね。

　さて、こういった摩擦の不思議な振る舞いは、どのようにして起きるのか？　が知りたいのですが、かんじんの断層の摩擦のメカニズムは、今のところ不明です。そこでまずは金属などを使った実験から、摩擦現象はどのように考えられているかを説明します。

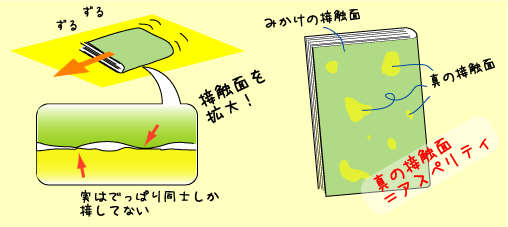　グリフィスクラックの時みたいに、不完全であることを前提として話をすすめるんですな。つまり摩擦表面は完璧な平面ではなくてビミョーな凸凹があって、そのでっぱり同士が噛み合って、全体を支えている。これがエッセンスです。上の図は部分接触を表現した物で、教科書に生えたカビじゃないゾ。

　　（Ｆ：引きずるのに必要な力　μ：摩擦係数　ｎ：垂直応力）である。

　ずばり！エッセンスは部分接触です。こいつが考え方の鍵を握ります。つまりいくら広い面からできていても、真の接触面というのはほんのちょこっとってわけです。右図のようにいくつかの点で接触していて、大半の部分はなーんにもしてないってわけです。で、この点の数が増えたり、もしくは各点の面積が増えるとトータルの摩擦が増加するってわけです。つまり、面は完璧な平面ではなく、ビミョーな凸凹があって、このデコ同士がぶつかって、全体を支えているってわけです。こいつをアスペリティと呼びます。で、これが例えば、大きな金属板同士を滑らすと考えますと、垂直応力が増えるとこのデコが上からの重さに耐えかねてグニャって変形します（これは弾性歪みでも永久歪みでも、どっちでもＯＫ）。そうすると接触面積が増えます。ほら、これで第１の法則がクリアですね。

　これを式で表しますと、
引きずるのに必要な力をＦ、部分接触しているアスペリティのトータルの面積をＡｒ、部分接触しているアスペリティの平均の剪断強度をＳ、

F=SAr（式２）

つまり全体の強度は、部分接触してる各点の強さとその合計で釣り合うってことですね。

　ところで、このＡｒっていうかアスペリティたる部分接触のエリアも垂直応力によって増加します。で、そのかみ合い具合といいますか、食い込み具合も、物質によって違うのでしょう。つまり軟らかければ凸は良く突き刺さるでしょうし、硬ければそうもいかんでしょう。この突き刺さり度は硬さによるので、これを貫入硬さ　ｐ、で表します。するってーと垂直応力をｎとした時、

Ar=n/p　

アスペリティは、ｎが増えると増加する　ｐが増えると（硬くなると）減る
で、アスペリティの大きさが表現できます。この式から次のようにもなります。

n=pAr　（式３）

垂直応力は　貫入硬さによって変化するアスペリティによって支えられる。
ともなります。
で、ここで最初の摩擦の法則を思い出しましょう。

Ｆ＝μｎ　（式１）

これに式３と式２を代入して、

F=μpAr=ArS

μ=ArS/pAr

μ =S/p　じゃあーん。摩擦係数がでてきました。

　これが摩擦係数μですって。うーん、なるほど。アスペリティがどれだけ食い込むか、そんで食い込んだアスペリティがどんだけ強いかってわけですね。

ま、簡単に言えば、分母は、貫入硬さが増す　→　食い込まない　→　摩擦係数は減る（分母が大きくなるからね）。分子は、剪断強度が増す　→　pは一定でも摩擦係数は増加する。

というわけで、摩擦係数ってのは、

凸（デコ）がどんだけ食い込むか？　と、
食い込んだ凸がどんだけ強いのか？

の２つのバランスによって決まるってことになります。

と、いうわけで上の式を絵に描くと

１）摩擦面は部分的な凸凹で接している。
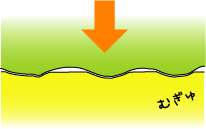
２）凸凹は押されると変形する。
３）だから上から押されると、より食い込んで接触面積が増える。
４）だから摩擦は、どんだけ食い込むか？と、それが、食い込んだ凸はどんだけ強いかか？によって決まります。

μってそういうことなのね。

まとめ　μとは何か？

　なんたってエッセンスは部分接触です。で、この部分接触エリアの増え具合は貫入硬さによっていて、あとはこの部分接触しているエリアの剪断強度が大きければ摩擦係数が増えるってわけですね。で、垂直応力が増えると、凸がいっそう食い込むので、全体の摩擦強度は増します。垂直応力がもっと増えると、凸もどんどん食い込みます。で、最後にはどうなってしまうのかと言えば、ついには部分接触が全面接触になってしまうことでしょう。するってーと摩擦の法則が成り立つのも、もはやここまで。ぅぅぅ。

　え？それでいいの？　って思うかもしれませんが、それでいーんです。だって摩擦強度が垂直応力に比例して無限に強くなってもヘンでしょ？

今回は下記の教科書を参考にさせていただきました。
ショルツ　著／柳谷俊　訳　　「地震と断層の力学」