地震と活断層（７）：必殺グリフィスクラック

update 2003.7/8

いきなりエッセンス

　　この前提が納得いけば、もう山場は過ぎたも同然

　なんでもいいから物体に応力をかけて、かけて、どんどんかけていくと、そのうち限界になってその物体は壊れてしまいます。唐突に壊れてしまう。そんな物の力学って何よ？！　なにせ”突然バキッ”　でしょ。そんな物どう扱っていいのかわからないじゃない。　うーん。では、どうするか？　それは次のように考えるのです。

　「世の中に完全無欠の物体なんてない。内部は無数の目には見えないクラックだらけである。そのクラックのどれかに剪断応力がかかり、クラックが滑り、そしてクラックが成長して、ついには全体の破壊に至る。」

ってなわけです。完全無欠の物は無い。「クラックだらけだ！」これがポイントです。では、

どんなクラックが滑りはじめるのか？
どうやって成長するのか？

について考えてみましょう。

破壊＝すべり？

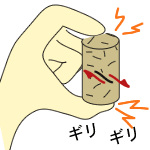うまい向きの傷がすべり始めてついに全体が破壊する。

　　　まず、このチョークにもきっとたくさんのクラックが入っているでしょう。それをこうやってギューっと押します。そしてこの中のあるクラックが滑りはじめます。　外のある方向から物を押して滑らせるんだけど、例えばこの教科書を手で押して滑らす場合、どの方向から押したらうまく滑るでしょうか？　もちろん斜めから押した時ですね。垂直に押しても単にページがぎゅーっと詰まるだけで、滑りは発生しませんね。すなわちこのチョークの中のクラックも外力に対して斜め向きのやつが滑りはじめます。垂直向きのクラックは押されて閉じるのみです。

応力の集中

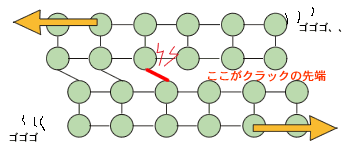応力集中の図　　究極に微細なクラックの先端。すでに原子の手が切れた部分は、応力を支えられません（当たり前だ。手がないんだから、、）。　その分の応力まで全部がクラック先端に集中、、、弱いものいじめですな。

　とはいえクラックが、ほんのちょっと滑る程度では不十分で、クラックがどんどん成長してこそ物体全体の破壊や巨大な断層の活動になるのです。ではどうやって成長して行くのかを考えましょう。

まず、究極に微小なクラックを想定します。なにせ原子の手のつなぎ目の切れ目という究極のクラック。これを左右から引っ張ります。切れ目のないフツーの部分はちゃーんと引っ張り応力を原子同士の手でひっぱってがんばってます。でも切れ目の部分は引っぱりをがんばることはできません。なにせ手をつないでないんだから。そして往々にしてこの引っぱりの力は、クラックの端に集中します。そして必要以上に応力がクラックの端に集中した結果、この手が切れてしまいます。あーあ。

　しかも事態は一向に改善されないどころか、よけいに悪くなってしまいました。クラックの長さが伸びて、次の原子にはより大きな負担がかかります。まるで職場で誰かが過労で倒れて、その人の分だけ仕事が増えて次の人が倒れるような状況です。もうドミノ倒しのように、その課が、そして部が、ゆくゆくは会社全体が、、、、　これが応力集中による効果です。ちょっとしたクラックのおかげで、物質本来の強度よりもはるかに弱い力で壊れてしまうのです。

　さてここまで聞いて、物質にちょっとしたクラックがあって、うまい方向から力をかければ簡単に壊せるんだなってわかったことでしょう。そしてそれは本来の強度よりもはるかに物質を弱くさせていることを理解したことでしょう。特に鋭い切れ目ほどいけません。応力集中が著しく生じます。だから素人が勝手にカッチョイーからといって車やスクーター、それに理学部棟の屋上なんかに切れ目なんていれちゃいけません。重大な結果を招く可能性があります。

今日のハイライト！

物の表面には、表面があるというだけでエネルギーが存在するのです、、、わかりますか？

　で、この応力集中を使えば、比較的小さな力で物質を破壊することができるんだってことがわかったでしょう。でも、それだけだったら全ての物質には無数のクラックがあるはずなので、全ての物質は果てしなく弱く、破壊しまくりな気がしませんか？　でもそうではない。そう、クラックがどんどん成長するには、もう一つ条件があるのです。

それは「弾性エネルギーが表面エネルギーよりも大きい必要がある」ってやつです。

　　それって何？　って感じですね。弾性エネルギーは比較的解り易いです。例えばプラスチック定規をぐーっっっと曲げた時に元に戻ろうとする力ですね（ストレスがたまらねーの章参照）。原子同士の手がバネのように延び縮みすることに起因します。一方の表面エネルギーって何よ？　これはあまり聞き覚えがありません。本来、物質の表面それ自体がエネルギーを持っているというのです。はああ？？　って感じですね。水滴が丸くなるように、本当は表面積を小さくしたがっているというのです。だからヘンなデコボコは嫌いで、スキ有らば表面エネルギーの小さい方になりたいといのです。だからガラスや金属を熱して柔らかくすると水滴のように丸くなるというのです。そうなりたがっている。うううん。わかる？？　

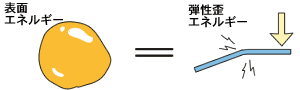　そもそも表面エネルギーが直感的に納得しにくいのに、それが弾性歪エネルギーと等価だなんて言われてもねえ？　って感じでしょうか。でも、こういう大胆な発想のジャンプが偉大なんでしょうな。

　　一方、これが物の破壊の場合、例えばこのチョークがこんな風に　バキッ　と割れると、それまでなかった表面が発生します。きっとこれはチョークには嫌な状態。表面エネルギーが増えてしまったああ、ってな状態なのね。では、増えたエネルギーはどこから来たかと言うと、破壊する直前にチョークががんばっていた時の弾性エネルギーが変換されたのですね。ここがミソです。弾性エネルギーが表面エネルギーを超えると破壊する。弾性エネルギーが、どんどん表面エネルギーになって、クラックが成長し続けるんですね。超えなければ破壊がスタートしない。これが完全無欠だったら、かなり強固なんだけど（100倍くらい！）、ある特定の方向のクラックの端では、応力集中が激しく生じている。で、クラックが成長するための表面エネルギーを弾性エネルギーが超えれば、クラックは成長して破壊に至るって考えるのです。

以上のストーリーはグリフィスという若僧（当時）の考えたことで、最初に仮定した微少なクラックのことをグリフィスクラックと呼ぶのです。破壊力学の教科書には必ず載っている基本中の基本の考え方です。

まとめ

　まあ、簡単にまとめますと、外見とはうらはらに欠陥だらけで、そこをつつくと案外脆い。そして、とんがってても本当は丸くなりたがっている。ってわけですね（よけーわからん）

今回は下記の教科書を参考にさせていただきました。
Ｊ．Ｅ．ゴードン著　土井恒成　訳　「強さの秘密」